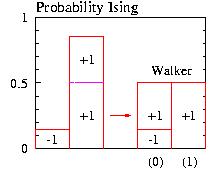
- Figure: The Ising probability
and the walker probability. The walker algorithm provide
a uniform probability for 2 states. First we choose
randomly the "box" (0) or (1). Then using an Alias
we can get the + or - state. More ...
|
|
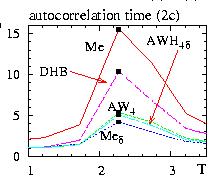
- Figure: comparison of the autocorrelation time for various algorithms
for the two dimensional ferromagnetic square lattices (2c), L=10
The critical temperatures are shown by the squares
- AW4=Alias Walker for 4 spins
- AWH4=Alias Walker Hasting for 4 spins
- DHB=Direct Heat-Bath
- Me =Metropolis
- Me d = Restricted Metropolis
|
|
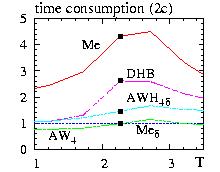
- Figure: comparison of the time of simulation for various algorithms
for the two dimensional ferromagnetic square lattices (2c), L=10
The critical temperatures are shown by the squares
- AW4=Alias Walker for 4 spins
- AWH4=Alias Walker Hasting for 4 spins
- DHB=Direct Heat-Bath
- Me =Metropolis
- Me d = Restricted Metropolis
|
|
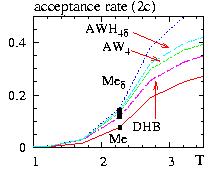
- Figure: comparison of the rate of simulation for various algorithms
for the ferromagnetic square lattices (2c), L=10
The critical temperatures are shown by the squares
- DHB=Direct Heat-Bath
- AW4=Alias Walker for 4 spins
- AWH4=Alias Walker Hasting for 4 spins
- Me =Metropolis
- Me d = Restricted Metropolis
|
|



